Compromesso bias-varianza

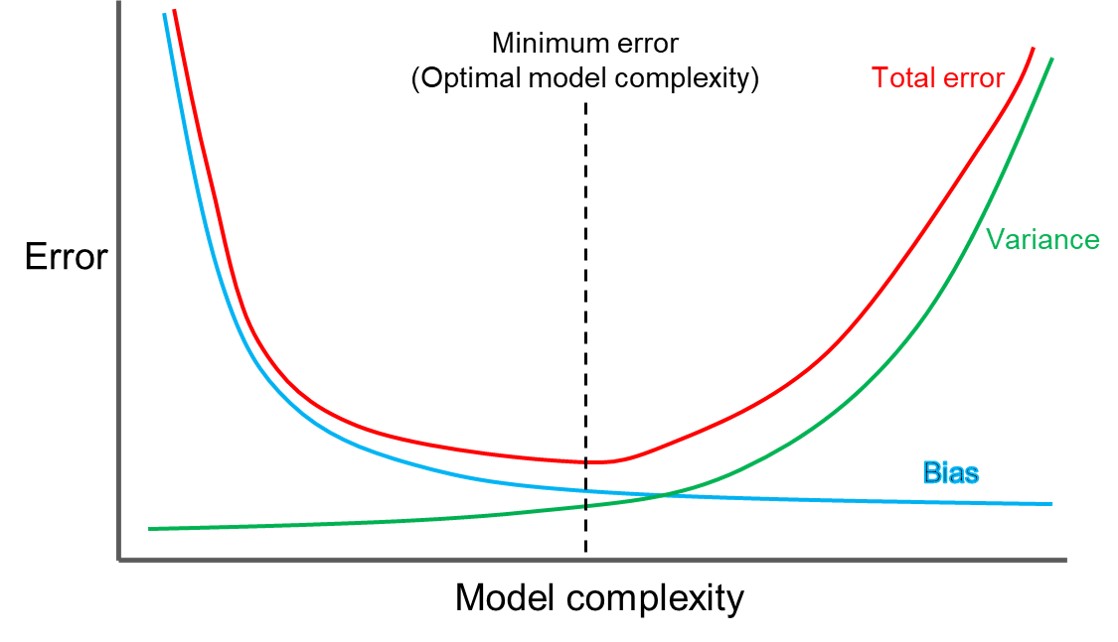
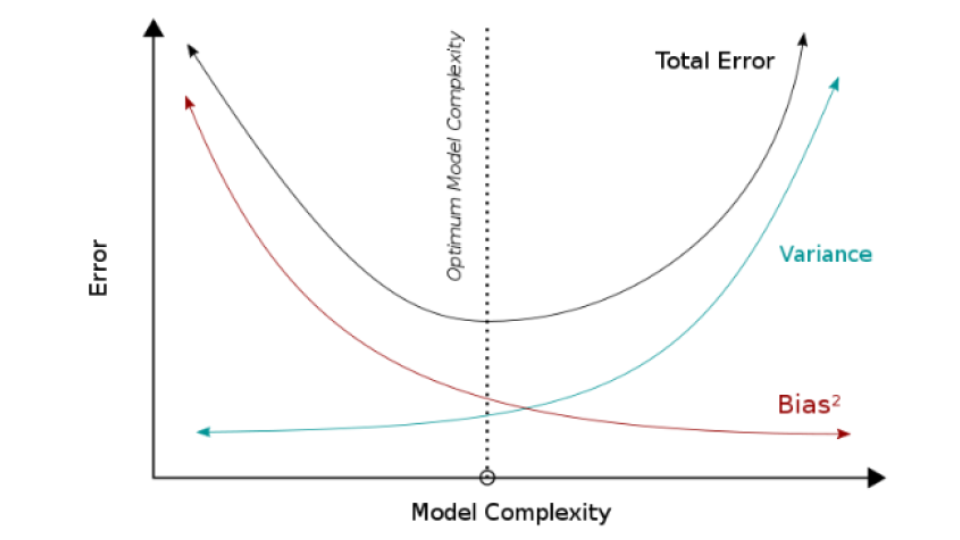
Nella statistica e nell'apprendimento automatico, il compromesso bias-varianza (in inglese bias-variance tradeoff) è la proprietà di un modello secondo cui la varianza del parametro stimato tra i campioni può essere ridotta aumentando il bias nei parametri stimati. Il dilemma o problema della bias-varianza sta nel conflitto nel tentativo di minimizzare contemporaneamente queste due fonti di errore che impediscono agli algoritmi di apprendimento supervisionato di generalizzare oltre il loro insieme di addestramento (o training set):

• L'errore di bias è un errore derivante da presupposti errati nell'algoritmo di apprendimento. Un elevato bias può far sì che un algoritmo manchi le relazioni rilevanti tra le caratteristiche e gli output di destinazione (underfitting).
• La varianza è un errore dovuto alla sensibilità a piccole fluttuazioni nel training set. Un'elevata varianza può derivare da un algoritmo che modella il rumore casuale nei dati di addestramento (overfitting).

La scomposizione bias-varianza è un modo per analizzare l'errore di generalizzazione atteso di un algoritmo di apprendimento rispetto a un particolare problema come somma di tre termini, il bias, la varianza e una quantità chiamata errore irriducibile, risultante dal rumore nel problema stesso.

Motivazione

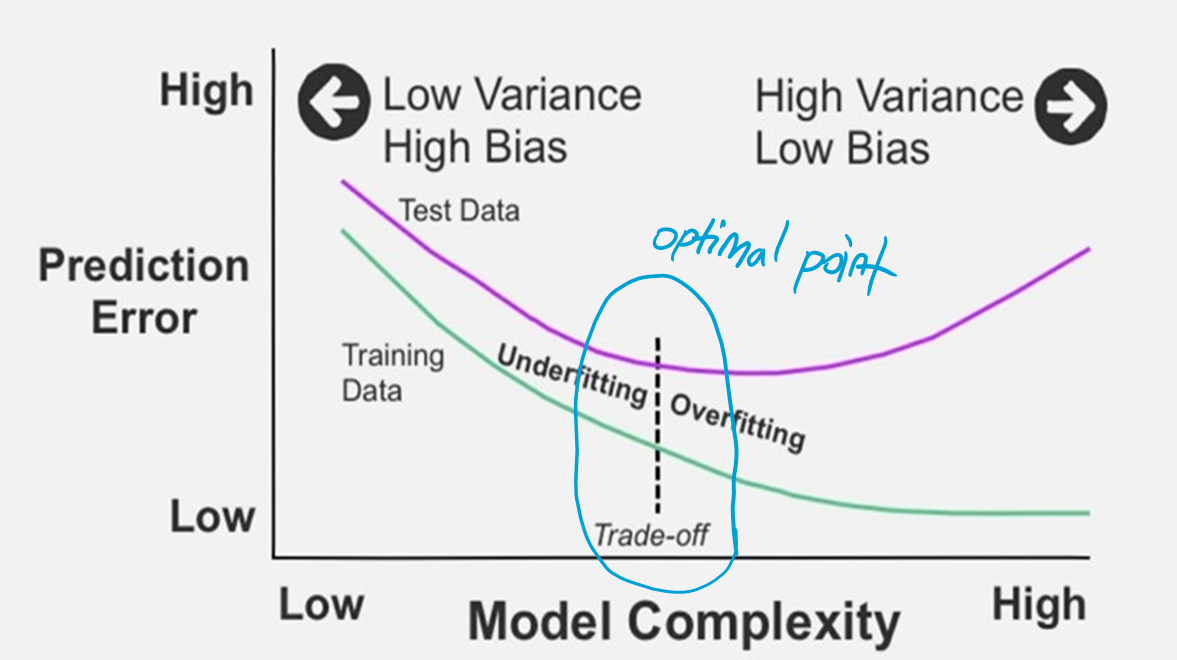
Il compromesso bias-varianza è un problema centrale nell'apprendimento supervisionato. Idealmente, si vuole scegliere un modello che catturi con precisione le regolarità nei suoi dati di addestramento, ma che generalizzi anche bene ai dati non visti. Sfortunatamente, in genere è impossibile fare entrambe le cose contemporaneamente. I metodi di apprendimento ad alta varianza possono essere in grado di rappresentare bene il loro set di training, ma rischiano di adattarsi eccessivamente ai dati rumorosi o non rappresentativi. Al contrario, gli algoritmi con alto bias producono in genere modelli più semplici che potrebbero non riuscire a catturare regolarità importanti (vale a dire underfit) nei dati. Nel primo caso si parla di overfitting e nel secondo di underfitting.

È una comune fallacia presumere che i modelli complessi debbano avere un'elevata varianza; mentre i modelli ad alta varianza sono "complessi" in un certo senso, non è necessariamente vero il viceversa. Inoltre, bisogna stare attenti a come definire la complessità: in particolare, il numero di parametri utilizzati per descrivere il modello è una misura scarsa della complessità. Ciò è illustrato dal seguente esempio. Il modello ${\displaystyle f_{a,b}(x)=a\sin(bx)}$ ha solo due parametri (${\displaystyle a,b}$), ma può interpolare qualsiasi numero di punti oscillando con una frequenza sufficientemente alta, risultando sia in un elevato bias che in un'elevata varianza.

Intuitivamente, la distorsione viene ridotta utilizzando solo le informazioni locali, mentre la varianza può essere ridotta solo facendo la media su più osservazioni, il che significa intrinsecamente utilizzare le informazioni provenienti da una regione più ampia. Per un esempio illuminante, vedere la sezione sui vicini più vicini o la figura a destra. Per bilanciare la quantità di informazioni utilizzate dalle osservazioni vicine, un modello può essere "lisciato" tramite regolarizzazione esplicita, come lo shrinkage (restringimento).

Scomposizione bias-varianza dell'errore quadratico medio

Si supponga di avere un training set ${\displaystyle D=\{(x_{1},y_{1})\dots ,(x_{n},y_{n})\}}$, composto da un insieme di punti ${\displaystyle x_{1},\dots ,x_{n}}$ e valori reali ${\displaystyle y_{i}}$ associato a ciascun punto ${\displaystyle x_{i}}$, e si assuma l'esistenza di una funzione ${\displaystyle y=f(x) \varepsilon }$, dove il rumore ${\displaystyle \varepsilon }$ ha media nulla e varianza ${\displaystyle \sigma ^{2}}$.

L'obiettivo è trovare una funzione ${\displaystyle {\hat {f}}(x;D)}$ che approssima la vera funzione ${\displaystyle f(x)}$ nel miglior modo possibile, mediante un algoritmo di apprendimento basato sul training set. Nello specifico, "nel miglior modo possibile" significa richiedere che l'errore quadratico medio tra ${\displaystyle y}$ e ${\displaystyle {\hat {f}}(x;D)}$, ovvero ${\displaystyle (y-{\hat {f}}(x;D))^{2}}$, sia minimo, sia per ${\displaystyle x_{1},\dots ,x_{n}}$ sia per i punti al di fuori del campione. Naturalmente, dal momento che i valori ${\displaystyle y_{i}}$ contengono rumore ${\displaystyle \varepsilon }$, ogni funzione che approssima avrà un "errore irriducibile".

Trovare una ${\displaystyle {\hat {f}}}$ che generalizza a punti al di fuori del set di addestramento può essere fatto con uno qualsiasi degli innumerevoli algoritmi utilizzati per l'apprendimento supervisionato. Ad ogni modo, per ogni funzione ${\displaystyle {\hat {f}}}$, è possibile il suo errore atteso su un nuovo campione ${\displaystyle x}$ come segue:

${\displaystyle \operatorname {E} _{D,\varepsilon }{\Big [}{\big (}y-{\hat {f}}(x;D){\big )}^{2}{\Big ]}={\Big (}\operatorname {Bias} _{D}{\big [}{\hat {f}}(x;D){\big ]}{\Big )}^{2} \operatorname {Var} _{D}{\big [}{\hat {f}}(x;D){\big ]} \sigma ^{2}}$

dove

${\displaystyle \operatorname {Bias} _{D}{\big [}{\hat {f}}(x;D){\big ]}=\operatorname {E} _{D}{\big [}{\hat {f}}(x;D){\big ]}-f(x)}$

e

${\displaystyle \operatorname {Var} _{D}{\big [}{\hat {f}}(x;D){\big ]}=\operatorname {E} _{D}[{\big (}\operatorname {E} _{D}[{\hat {f}}(x;D)]-{\hat {f}}(x;D){\big )}^{2}].}$

Il valore di espettazione spazia su diverse scelte del set di allenamento ${\displaystyle D=\{(x_{1},y_{1})\dots ,(x_{n},y_{n})\}}$, tutti campionati dalla stessa distribuzione congiunta ${\displaystyle P(x,y)}$. I tre termini rappresentano:

• il quadrato del bias del metodo di apprendimento, che può essere pensato come l'errore causato dalle ipotesi semplificative incorporate nel metodo. Ad esempio, quando si approssima una funzione non lineare ${\displaystyle f(x)}$ utilizzando un metodo di apprendimento per modelli lineari, ci saranno errori nelle stime ${\displaystyle {\hat {f}}(x)}$ a causa di questa ipotesi;
• la varianza del metodo di apprendimento, o, intuitivamente, quanto il metodo di apprendimento ${\displaystyle {\hat {f}}(x)}$ si muoverà intorno alla sua media;
• l'errore irriducibile ${\displaystyle \sigma ^{2}}$ .

Poiché tutti e tre i termini non sono negativi, l'errore irriducibile forma un limite inferiore all'errore atteso su campioni invisibili.

Più complesso è il modello ${\displaystyle {\hat {f}}(x)}$ vale a dire, più punti dati acquisirà e minore sarà la distorsione. Tuttavia, la complessità farà "spostare" maggiormente il modello per acquisire i punti dati, e quindi la sua varianza sarà maggiore.

Derivazione

La derivazione della scomposizione bias-varianza per l'errore al quadrato procede come segue. Per comodità di notazione, si abbrevia ${\displaystyle f=f(x)}$, ${\displaystyle {\hat {f}}={\hat {f}}(x;D)}$ e si lascia cadere il pedice ${\displaystyle D}$ sui nostri operatori di aspettativa. Innanzitutto, per definizione, per qualsiasi variabile casuale ${\displaystyle X}$, si ha

${\displaystyle \operatorname {Var} [X]=\operatorname {E} [X^{2}]-\operatorname {E} [X]^{2}.}$

Riordinando, si ottiene:

${\displaystyle \operatorname {E} [X^{2}]=\operatorname {Var} [X] \operatorname {E} [X]^{2}.}$

Da quando ${\displaystyle f}$ è deterministico, cioè indipendente da ${\displaystyle D}$ ,

${\displaystyle \operatorname {E} [f]=f.}$

Così, dato ${\displaystyle y=f \varepsilon }$ e ${\displaystyle \operatorname {E} [\varepsilon ]=0}$ (perché ${\displaystyle \varepsilon }$ è rumore), implica ${\displaystyle \operatorname {E} [y]=\operatorname {E} [f \varepsilon ]=\operatorname {E} [f]=f.}$

Inoltre, poiché ${\displaystyle \operatorname {Var} [\varepsilon ]=\sigma ^{2},}$

${\displaystyle \operatorname {Var} [y]=\operatorname {E} [(y-\operatorname {E} [y])^{2}]=\operatorname {E} [(y-f)^{2}]=\operatorname {E} [(f \varepsilon -f)^{2}]=\operatorname {E} [\varepsilon ^{2}]=\operatorname {Var} [\varepsilon ] \operatorname {E} [\varepsilon ]^{2}=\sigma ^{2} 0^{2}=\sigma ^{2}.}$

In definitiva, poiché ${\displaystyle \varepsilon }$ e ${\displaystyle {\hat {f}}}$ sono indipendenti,

${\displaystyle {\begin{aligned}\operatorname {E} {\big [}(y-{\hat {f}})^{2}{\big ]}&=\operatorname {E} {\big [}(f \varepsilon -{\hat {f}})^{2}{\big ]}\\[5pt]&=\operatorname {E} {\big [}(f \varepsilon -{\hat {f}} \operatorname {E} [{\hat {f}}]-\operatorname {E} [{\hat {f}}])^{2}{\big ]}\\[5pt]&=\operatorname {E} {\big [}(f-\operatorname {E} [{\hat {f}}])^{2}{\big ]} \operatorname {E} [\varepsilon ^{2}] \operatorname {E} {\big [}(\operatorname {E} [{\hat {f}}]-{\hat {f}})^{2}{\big ]} 2\operatorname {E} {\big [}(f-\operatorname {E} [{\hat {f}}])\varepsilon {\big ]} 2\operatorname {E} {\big [}\varepsilon (\operatorname {E} [{\hat {f}}]-{\hat {f}}){\big ]} 2\operatorname {E} {\big [}(\operatorname {E} [{\hat {f}}]-{\hat {f}})(f-\operatorname {E} [{\hat {f}}]){\big ]}\\[5pt]&=(f-\operatorname {E} [{\hat {f}}])^{2} \operatorname {E} [\varepsilon ^{2}] \operatorname {E} {\big [}(\operatorname {E} [{\hat {f}}]-{\hat {f}})^{2}{\big ]} 2(f-\operatorname {E} [{\hat {f}}])\operatorname {E} [\varepsilon ] 2\operatorname {E} [\varepsilon ]\operatorname {E} {\big [}\operatorname {E} [{\hat {f}}]-{\hat {f}}{\big ]} 2\operatorname {E} {\big [}\operatorname {E} [{\hat {f}}]-{\hat {f}}{\big ]}(f-\operatorname {E} [{\hat {f}}])\\[5pt]&=(f-\operatorname {E} [{\hat {f}}])^{2} \operatorname {E} [\varepsilon ^{2}] \operatorname {E} {\big [}(\operatorname {E} [{\hat {f}}]-{\hat {f}})^{2}{\big ]}\\[5pt]&=(f-\operatorname {E} [{\hat {f}}])^{2} \operatorname {Var} [\varepsilon ] \operatorname {Var} {\big [}{\hat {f}}{\big ]}\\[5pt]&=\operatorname {Bias} [{\hat {f}}]^{2} \operatorname {Var} [\varepsilon ] \operatorname {Var} {\big [}{\hat {f}}{\big ]}\\[5pt]&=\operatorname {Bias} [{\hat {f}}]^{2} \sigma ^{2} \operatorname {Var} {\big [}{\hat {f}}{\big ]}.\end{aligned}}}$

Infine, la funzione obiettivo MSE si ottiene prendendo il valore di aspettativa ${\displaystyle x\sim P}$:

${\displaystyle {\text{MSE}}=\operatorname {E} _{x}{\bigg \{}\operatorname {Bias} _{D}[{\hat {f}}(x;D)]^{2} \operatorname {Var} _{D}{\big [}{\hat {f}}(x;D){\big ]}{\bigg \}} \sigma ^{2}.}$

Note